HTML
-
Lagrangian stochastic (LS) models are widely used for wind field simulation, incorporating the stochastic process and statistical information on wind velocities under different field conditions (Rossi et al., 2004). LS models play a particularly important role in managing atmospheric pollutants (Wang et al., 2008; Fattal and Gavze, 2014; Leelössy et al., 2016; Asadi et al., 2017), biological particles (e.g., weed pollen) (Wang and Yang, 2010a, b), and the like. These management efforts are achieved by simulating particle dispersion behaviors caused by the force of wind in the surface layer (Wilson and Shum, 1992; Aylor and Flesch, 2001). Besides, LS models are required to follow the well-mixed condition criterion (Thomson and Wilson, 2012), which states that if the particles of tracers are well mixed initially, they should remain so.
Previously, Wilson and Shum (1992) assumed that the wind velocity in the surface layer follows the Gaussian distribution, and they successfully developed a Gaussian LS model that was proven to be satisfactory to the well-mixed condition criterion set by Thomson (1987). Their model also considers the inhomogeneity of the wind field—namely, the mean and variance of targeted Gaussian distribution changes at different heights.
However, their Gaussian distribution assumption was not satisfied because the measured wind velocity distribution in the surface layer in general was observed to be non-Gaussian (i.e., skewness and kurtosis of the wind velocity distribution did not equal 0 and 3, respectively) (Legg, 1983; Flesch and Wilson, 1992). Therefore, the researchers were challenged to build a non-Gaussian LS model and to use higher-order statistics (skewness and kurtosis) to evaluate the accuracy of the wind field simulation (Du, 1997; Rossi et al., 2004).
Since then, some non-Gaussian LS models have been proposed for wind field simulation in the surface layer (Legg, 1983; De Baas et al., 1986; Sawford and Guest, 1987) with the understanding that their generated velocity distribution cannot be consistent with the measured non-Gaussian distribution (Flesch and Wilson, 1992; Wilson and Sawford, 1996). Thus, their models are counter to the well-mixed condition criterion (Flesch and Wilson, 1992).
Meanwhile, non-Gaussian LS models were largely studied for the wind field in the convective boundary layer (Bærentsen and Berkowicz, 1984; Luhar and Britter, 1989; Weil, 1990; Luhar et al., 1996; Cassiani et al., 2015). In general, they solved this issue of non-Gaussian field simulation by combining two random variables following Gaussian distributions, which reflects an interaction between an updraft and downdraft wind turbulent velocities (Luhar et al., 1996; Cassiani et al., 2015). Nevertheless, their models cannot be generalized for simulation in the surface layer (Flesch and Wilson, 1992).
Later, Flesch and Wilson (1992) developed a surface-layer non-Gaussian LS model under the well-mixed condition framework. However, their dispersion simulation results were no better than results from the Gaussian LS model proposed by Wilson and Shum (1992) because of the difficulty in formulating correct non-Gaussian velocity distributions (Flesch and Wilson, 1992). This obstacle is due to the changing velocity distribution in the wind field (i.e., non-stationarity). Specifically, the wind field in the surface layer displays a strong and differing non-Gaussian behavior at each small-scale observation (Pope and Chen, 1990; Katul et al., 1994), e.g., in a 30-min period. Therefore, the non-stationarity of the wind field requires that the simulated velocity distribution of an LS model be adaptive to the measured wind velocity distribution in different observation periods.
To solve this non-stationarity problem, a three-dimensional (3D) LS model (Wang et al., 2008; Wang and Yang, 2010b) was developed based on the Gaussian LS model proposed by Wilson and Shum (1992). This 3D LS model adjusts the mean and variance of the simulated wind velocity in different short time periods to adapt to the changing velocity distribution in the field. However, the 3D LS model still assumes that the field velocity distribution is Gaussian, and a non-Gaussian, non-stationary LS model remains to be developed.
In this article, we present a non-Gaussian LS model that is built upon the Gaussian 3D inhomogeneous, non-stationary LS model (shortened to the Gaussian model hereafter) by Wang et al. (2008). We incorporate correct skewness and kurtosis in the simulated wind velocities by combining them with controllable non-Gaussian random variables. A non-Gaussian variable is supported by a combination of two Gaussian random number generators with parameters that are produced by a heuristic approach.
The proposed model is verified by the Cooperative Atmospheric Surface Exchange Study, October 1999 (CASES-99) experimental data (Poulos et al., 2002) which contain 3584 sets of measured 3D velocities in the field at eight different heights. We simulated these measured velocities with our non-Gaussian model and the original Gaussian model. We also conducted linear regression analysis on the statistical characteristics (mean, variance, skewness, kurtosis, friction velocity) of simulated wind velocities that are counter to the measured characteristics. The model performance is estimated by the slope (k) of a linear regressed line between the simulated and measured characteristics and the coefficient of determination (R2). A more accurate model generates both k and R2 close to 1 on all statistical characteristics. The experimental results show that:
● The distribution accuracy of wind velocities simulated by the proposed non-Gaussian model substantially outperforms that generated by the Gaussian model. The reason is that the non-Gaussian model can produce more accurate skewness and kurtosis (their k and R2 are close to 1) in the simulated velocities as compared to those produced by the Gaussian model (k and R2 are close to 0) while maintaining the accuracy in mean and variance of the Gaussian model.
● The improved skewness and kurtosis better simulate friction velocities (a coupling of 3D velocities) that are comparable to those measured, where k increases from 0.86 to 0.97, and R2 enhances from 0.67 to 0.95.
● The improved accuracy in skewness, kurtosis, and friction velocity can be stably generated by the proposed non-Gaussian model since the standard deviations of their k and R2 are close to 0 for 50 simulations. This result also indicates that the non-Gaussian model can better simulate wind field velocities and trajectories, as required by the well-mixed condition criterion.
● The proposed model can adapt to numerous types of non-Gaussian wind fields, in terms of a wide range of skewness–kurtosis combinations. Therefore, the model can meet the non-stationarity requirement in the field.
To analyze the necessity and utility of developing a non-Gaussian model, we investigated how the improved skewness and kurtosis (i.e., the third and fourth moments of the wind velocities, respectively) affect the wind/particle trajectory simulation. Results show that:
● In a one-dimensional (1D) homogeneous stationary field for wind trajectory simulation, the wind displacements (i.e., the final dispersion distances) converge to a Gaussian distribution. The skewness and kurtosis of simulated wind velocities can lead to a totally different displacement distribution because they heavily influence the variance of the displacement distribution, where velocity skewness and kurtosis have positive and negative effects, respectively, on the displacement variance.
● In a 3D inhomogeneous, non-stationary field for particle dispersion simulation, the non-Gaussian model with correctly simulated velocity skewness and kurtosis generates significantly different particle displacement distributions, leading to a substantial difference in particle concentrations as compared with the Gaussian model. The sensitivity of particle dispersion on velocity skewness and kurtosis implies the necessity of building a non-Gaussian model.
The remainder of this paper is organized as follows: Section 2 presents the background of the traditional Gaussian LS model and the proposed non-Gaussian LS model. Section 3 describes the experimental setup for wind field simulation. Section 4 provides the experimental results and discussion. Section 5 summarizes the study and its findings.
-
In this section, we first present the background of the LS model in section 2.1, then describe the theory of our non-Gaussian LS model in section 2.2, and finally provide the implementation details in section 2.3.
-
In a wind field simulation, the Gaussian LS models by Wilson and Shum (1992), Wang et al. (2008), and Wang and Yang (2010b) regard wind behavior as a random process in a sequence of short time steps (dt). In each step, wind velocities in the horizontal, cross, and vertical wind directions are represented by u, v, and w, respectively, as follows:
where
$\bar u\left(z \right)$ is the mean velocity along the wind speed at height z; σu, σv, and σw represent the standard deviations for three wind directions; vs is the settling velocity in the vertical direction; and qu, qv, and qw are random terms that follow the standard Gaussian distribution. These random terms are formed by a Markov chain that describes the historical effect of wind velocities at time t + dt, as indicated below:where
$\alpha = 1 - {\rm{d}}t/{\tau _L}$ ,$\beta = \sqrt {1 - {\alpha ^2}} $ , and$\gamma = 1 - \alpha $ are coefficients and dt = 0.025τL; the passive fluid Lagrangian time scale is τL = l/σw, and the term l is defined asand ru, rv, and rw are the dimensionless Gaussian random variables with a zero mean and unit variance. In addition, the term
${\tau _L}\dfrac{{{\rm d}{\sigma _w}}}{{{\rm d}z}}$ adjusts the vertical velocity at height z for the inhomogeneity of the wind field (Wilson et al., 1983); the appearance of rw in the Markov chain for qu gives rise to the correct coupling between u and w with coefficients${c_u} = - {u^{*2}}/\left({{\sigma _u}{\sigma _w}} \right)$ and${c_w} = \sqrt {1 - c_u^2} $ (Wilson and Shum, 1992), which also enables the model to produce the correct friction velocity (u*),${u^*} = {\left({{{\overline {u'w'} }^2} + {{\overline {v'w'} }^2}} \right)^{1/4}}$ . Detailed descriptions are provided by Wilson and Shum (1992) and Wang et al. (2008).In Eq. (1), the produced velocities (u, v, and w) are three components of Lagrangian velocity that traces individual fluid particles at one instant of time and position. According to the well-mixed condition criterion (Thomson and Wilson, 2012), the PDF statistics of the Lagrangian velocity simulated by a model at certain height should correctly and stably follow the PDF statistics of the measured Eulerian velocity, which tracks a volume of fluid particles at a fixed point of that height. However, the equations above can simulate only Gaussian wind velocities under the Lagrangian frame, but the measured Eulerian wind field is generally non-Gaussian (Legg, 1983; Flesch and Wilson, 1992).
To solve this problem, researchers (Legg, 1983; De Baas et al., 1986; Sawford and Guest, 1987) have built non-Gaussian LS models by replacing the Gaussian random forcing (ru, rv, and rw) in Eq. (2) with non-Gaussian random variables. However, such non-Gaussian random forcing is known to be incorrect because the generated velocity distribution cannot be consistent with the measured distribution, which is contrary to the well-mixed condition criterion (Flesch and Wilson, 1992; Wilson and Sawford, 1996).
To incorporate the non-Gaussian distribution into the LS model, we present a different non-Gaussian LS model, as described in sections 2.2 and 2.3. The proposed model aims to improve the distribution accuracy of simulated wind velocities in terms of skewness and kurtosis while maintaining other features of the traditional LS model.
-
For non-stationarity of the wind field, the Gaussian LS model divides the entire simulation time into a number of smaller time periods (T) (Wang et al., 2008; Wang and Yang, 2010b), such as 30 min. At time point t ∈ [0,T], the instantaneous wind velocity is represented by a random variable (u), as in Eq. (4), with a mean (
$\bar u$ ), standard deviation (σ), and a fluctuation term (q) following the standard Gaussian distribution:The variation in horizontal wind velocity (u) is used as one example because the cross (v) and vertical (w) wind velocities are similar. Specifically, in the form of Eq. (4), the cross-wind velocities have a mean
$\bar u = 0$ and a standard deviation σ=σv. For the vertical velocities, let Iw be the inhomogeneity term${\tau _L}\dfrac{{{\rm d}{\sigma _w}}}{{{\rm d}z}}$ . As Iw is independent of qwt and$r_w^{t + {\rm{d}}t}$ , w can be transformed as$w = {q_w}{\sigma _w} + \left({{I_w}{\sigma _w} - {v_s}} \right)$ with$q_w^{t + {\rm{d}}t} = \alpha q_w^t + \beta r_w^{t + {\rm{d}}t}$ , which shares the same form as Eq. (4).Our objective is to bring skewness and kurtosis into the LS model while maintaining other features of the original model. To reach this goal, we needed to incorporate skewness and kurtosis without affecting the mean (
$\bar u$ ) and standard deviation (σ). Therefore, we developed a new non-Gaussian random variable (p) with mean = 0, variance = 1, skewness ∈$\mathbb{R}$ , and kurtosis > 0. We combined p with q, as in Eq. (5), in which ε is a combination coefficient:This equation retains this feature of the Markov process from the original random variable q while adding a non-Gaussian feature from the new random variable p. To show how the formulated Eq. (5) can incorporate skewness and kurtosis while keeping its mean and variance unchanged, it was necessary to analyze the distribution characteristics of wind velocity in the equation.
First, Eq. (6) computes the mean velocity E[u] by substituting Eq. (5). Equation (5) calculates its variance V[u] in a similar process, where E[pq]=E[p]E[q] for the independence between p and q. We find that the mean E[u] and variance V[u] of velocity u remain unchanged regardless of whether it is a Gaussian (ε = 0) or non-Gaussian model (ε ≠ 0):
In the same way, the skewness S[u] and kurtosis K[u] are calculated as Eq. (8). The resulting skewness and kurtosis show that
$S\left[ u \right] \in \left( - {\left|S\left[ p \right]\right|, \left|S\left[ p \right] \right|} \right)$ and$K\left[ u \right] \in $ $\left[ {0, \max\left({K\left[ p \right],3} \right)} \right] $ for ε ∈ [0,1]. Therefore, by choosing a suitable combination coefficient ε, the new equation can incorporate controllable skewness and kurtosis into the wind velocity in terms of S[p] and K[p]. Because of this advantage, we applied the proposed combination method [Eq. (5)] to the traditional LS model in section 2.1: -
To generate the correct skewness and kurtosis of wind velocities while maintaining their mean and variance, Eq. (1) is modified by incorporating mutually independent random variables (pu, pv, and pw) with combination coefficients εj, according to Eq. (5):
where qj (j=u, v, w) are random variables following a standard Gaussian distribution, as defined in Eq. (2). Note that we moved the term
${\tau _L}\dfrac{{{\rm d}{\sigma _w}}}{{{\rm d}z}}$ from Eq. (2) to Eq. (4) to ensure that the incorporated non-Gaussian random variable pw does not affect the inhomogeneity in w. As in the traditional LS model, the appearance of pw in the horizontal velocity u (with coefficients cu and cw) is used to ensure the correctness of the coupling between u and w and the precision of simulated friction velocity. Section 4.1 investigates the necessity of placing the term pw in u, and the ability to maintain the historical effects of the Markov process.To obtain the correct target skewness SI,j(z) and kurtosis SI,j(z) for the j-direction wind velocities at height z, a non-Gaussian random variable pj was generated by a pseudo-random number generator (PRNG) with inputs SI,j(z) and SI,j(z). Section 2.3.1 describes the implementation details of PRNG. The undetermined combination coefficients εj and five parameters in PRNG are produced using a heuristic approach, as detailed in section 2.3.2.
-
The PRNG aims to incorporate the traditional LS model with different skewness and kurtosis, following the theory referred to in section 2.2. Generally, the PRNG inputs a pair of target skewness SI and kurtosis KI. It then generates a random number pt+dt with the correct skewness and kurtosis by using a combination of two Gaussian random number generators, as in Eq. (10)—one generator, gt+
dt, produces standard Gaussian random numbers; the other, vgt+dt+m, outputs Gaussian random numbers with the mean m and standard deviation v: We combined these two generators by controlling the proportion to be contributed to the random variable pt+dt. The proportion is managed by a division term d∈[1,+∞) and a uniform random variable
$r_0^{t + {\rm d}t} \in \left[ {0,1} \right]$ , as shown in Eq. (10). Specifically, when rt+dt0 is larger than 1/d, the first generator gt+dt serves the random variable pt+dt; otherwise, the second generator works.Moreover, the mean and variance of the generated random number are required to be 0 and 1, respectively, as referred to in section 2.2. Thus, the random variable pt+dt is normalized by its mean μp and standard deviation σp, as in Eq. (11). Note that the random variable pt+dt is finally multiplied by the sign of the target skewness SI to correct its skewness sign:
To generate the target skewness and kurtosis, the five uncertain parameters (m, v, d, μp, σp) and the corresponding combination coefficients (ε) were determined by a heuristic approach, which is introduced in section 2.3.2.
-
Learning an input-parameter relationship: To determine six unknown parameters (m, v, d, μp, σp, ε) for a pair of inputted target skewness SI and kurtosis KI, we need to know the relationship of SI and KI, to these six parameters. We learn this relationship by simulating the combination form of Eq. (9) and Eq. (12),
inputting four parameters (m, v, d, ε) with different values, and recording the skewness and kurtosis of a fixed number (18 000 in default) of random numbers
$\tilde u$ , where μp and σp equal the mean and standard deviation of generated random numbers, respectively. In this way, we can obtain many expected relationship recordings, as exemplified in Table 1.No. m v d ε μp σp S K 1 1.0 2.4 23 0.84 0.022 1.123 0.289 4.383 2 0.8 2.8 26 0.84 0.033 1.149 0.215 4.384 3 0.9 2.4 26 0.90 0.027 1.106 0.24 4.385 Table 1. An example of the input-parameter relationship.
To cover a wide range of skewness and kurtosis, we set mi∈[0, 10] and vi∈[0, 10] by using step 0.1 for both: di∈[2, 30] with step 1, and εi∈[0.1, 0.9] with step 0.01 for the inputs. Note that only the positive skewness (SI) is recorded because the negative condition can be handled by the sign (SI) in Eq. (11).
Moreover, to decrease the scale of recordings, we ruled out the ith recording, whose skewness and kurtosis are very close to those in the oth recording (o∈[1, m]). Specifically, for ∀i, o∈[1, m], and o>i, if |Si−So|≤0.02 and |Ki−Ko|≤0.02, then we excluded the ith recording because of its similarity to the oth recording.
Determine parameters for PRNG: To determine these six unknown parameters for a PRNG, we chose the ith recording that possesses the skewness, Si, and kurtosis, Ki, that are close to the target SI and KI. In other words, we searched these six parameters in the recordings with this objective:
${\rm{min}}\left({\left| {{S_I} - {S_i}} \right| + \left| {{K_I} - {K_i}} \right|} \right)$ . As illustrated in Table 1, if SI=0.285 and KI=4.383, the six parameters in the first row of the table are used for the PRNG because of their close values with S1=0.289 and K1=4.383.
2.1. Traditional Gaussian LS model
2.2. Modeling for a non-Gaussian wind field
2.3. Simulation for a non-Gaussian LS model
2.3.1. PRNG
2.3.2. Production of parameters
-
In this section, we first provide the studied wind field data in section 3.1, then describe the inputs of Gaussian and non-Gaussian LS models in section 3.2, and finally, present three designed simulation setups in section 3.3.
-
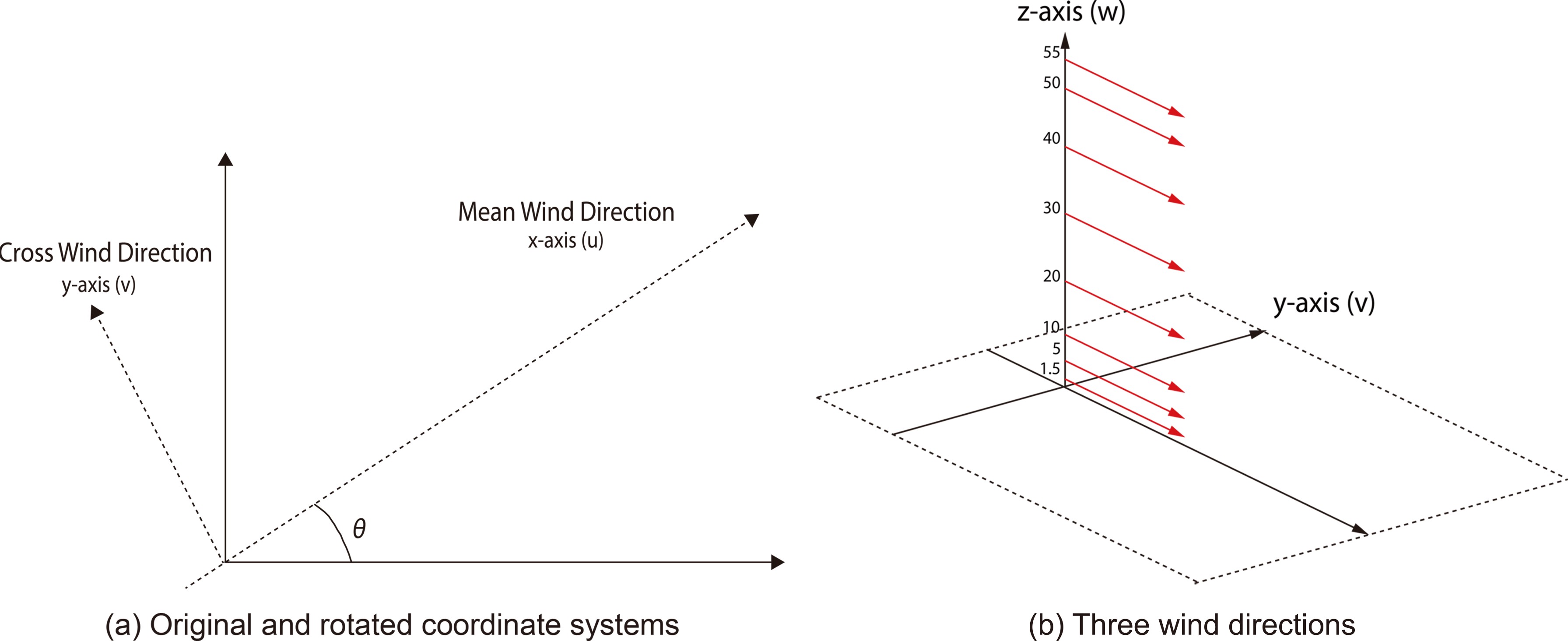
To evaluate the proposed non-Gaussian wind field algorithm, wind data were obtained from the main tower of the CASES-99 (Poulos et al., 2002). Three-dimensional wind velocities (u, v, w) and virtual temperatures were measured in the field with eight 10-Hz sonic anemometers placed at eight different heights (z) (Fig. 1b).
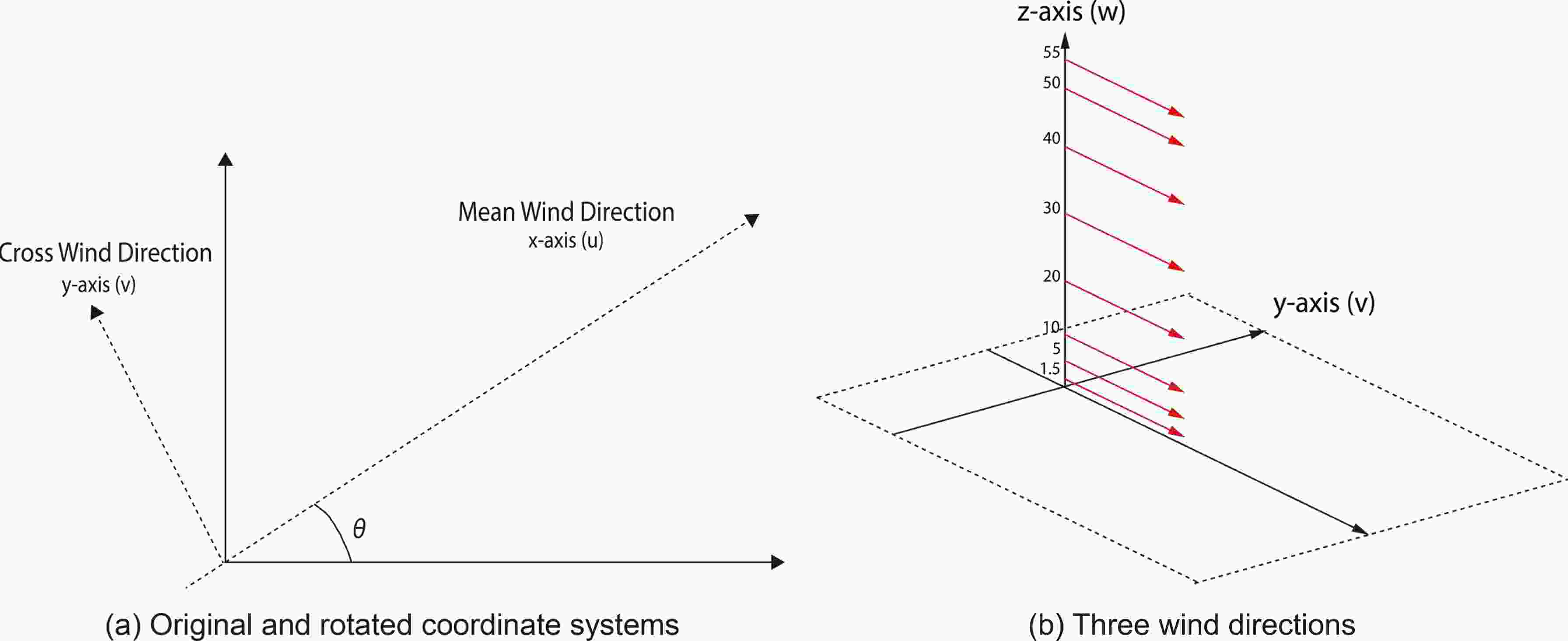
Figure 1. Rotated coordinate systems, and eight heights for measuring wind data in the CASES-99 project. Units: m.
We obtained 21 days (6–26 October) of daytime (0700 to 1900 UTC, 12 hours) wind data in CASES-99. To conduct atmospheric turbulence analysis and modeling, a short time period, 30 to 60 min, is commonly used to divide wind data into shorter periods (Moncrieff et al., 2004). In analyzing turbulence, such a time period can be sufficient to adequately sample all the motions that contribute to the atmospheric parameters to be obtained (e.g., mean, variance, skewness, and kurtosis). Also, an overly long period might produce irrelevant signals, affecting measurements (Moncrieff et al., 2004). Since a 30-min sampling period is commonly used (Aubinet et al., 2001; Mammarella et al., 2009; Eugster and Plüss, 2010), we divided one-day wind data into 48 30-min periods (504 periods in total). However, we excluded 56 periods recorded with wind velocity errors, i.e., NaN values, for problems caused by anemometers, including the periods in 10 October (0930–1200 and 1430–1900), 12 October (0700–0800), 13 October (0730–1900), and 14 October (0700–1500). As each period contains data for eight different heights, CASES-99 provides a total of 3584 (8 heights×448 periods) useful datasets.
For each dataset, the measured horizontal and crosswind velocities are rotated to a mean wind direction, as in Wesely (1971), and illustrated in Fig. 1a. In addition, atmospheric parameters denoting atmospheric conditions are calculated from each dataset, including friction velocity (u*), atmospheric stability (L), wind direction (θ), mean wind speed (
$\bar u$ ), and distribution characteristics (standard deviation, skewness, kurtosis) of the wind velocities. Table 2 shows the ranges of atmospheric conditions measured at eight heights.Height
z (m)Skewness Kurtosis Friction Velocity
u* (m s−1)Atmospheric Stability
L (m)Wind Direction
θ (°)Mean Wind Speed
$\bar u$ (m s−1)Variance u (m s−1) v (m s−1) w (m s−1) u (m s−1) v (m s−1) w (m s−1) u (m s−1) v (m s−1) w (m s−1) 1.5 −0.49 to 1.37 −1.23 to 1.03 −0.16 to 0.72 2.00 to 6.57 1.99 to 7.01 2.97 to 6.48 0.07 to 0.77 −883.91 to −0.27 1.74 to 359.99 0.26 to 7.22 0.08 to 3.66 0.07 to 3.20 0.01 to 0.73 5 −1.39 to 1.23 −1.23 to 1.43 −0.39 to 0.91 1.75 to 7.51 1.79 to 6.36 2.71 to 6.95 0.07 to 0.77 −565.75 to 216.90 0.40 to 359.68 0.31 to 9.56 0.12 to 4.50 0.06 to 4.44 0.03 to 0.89 10 −0.79 to 1.22 −1.30 to 1.52 −1.53 to 1.05 1.67 to 6.24 1.67 to 6.14 2.44 to 6.55 0.07 to 0.91 −508.85 to −0.18 0.41 to 359.58 0.28 to 9.79 0.06 to 3.77 0.04 to 4.27 0.04 to 1.29 20 −0.95 to 1.07 −1.13 to 1.74 −0.73 to 2.35 1.55 to 5.23 1.76 to 6.89 1.42 to 6.77 0.07 to 1.07 −1234.40 to 21.10 0.03 to 359.80 0.18 to 15.23 0.08 to 9.51 0.08 to 5.81 0.04 to 1.28 30 −0.98 to 1.04 −1.18 to 1.30 −0.48 to 1.45 1.48 to 7.16 1.81 to 5.74 2.15 to 7.14 0.08 to 1.00 −1082.30 to 189.70 0.01 to 359.50 0.13 to 13.44 0.08 to 4.71 0.07 to 5.30 0.04 to 0.98 40 −1.01 to 1.06 −1.25 to 1.44 −0.31 to 1.20 1.45 to 5.38 1.65 to 6.67 2.13 to 5.74 0.06 to 1.04 −3859.30 to 553.70 0.65 to 359.09 0.25 to 14.43 0.06 to 5.11 0.07 to 6.05 0.04 to 1.21 50 −1.22 to 1.21 −1.46 to 1.27 −0.21 to 1.41 1.61 to 4.94 1.72 to 6.69 1.95 to 6.98 0.04 to 1.00 −733.29 to 663.85 0.42 to 359.40 0.38 to 14.21 0.06 to 4.52 0.13 to 5.64 0.10 to 1.20 55 −1.29 to 1.13 −1.30 to 1.25 −0.56 to 1.37 1.55 to 5.94 1.67 to 5.75 1.92 to 7.64 0.09 to 1.12 −1130.40 to 1018.70 0.16 to 359.18 0.52 to 14.94 0.07 to 4.63 0.07 to 5.86 0.03 to 1.47 Table 2. The ranges of measured atmospheric conditions for each height (z) in three wind directions (u, v, w).
-
To simulate wind velocities for an atmospheric condition, the inputs of a Gaussian model include the initial height (z), friction velocity (u*), wind direction (θ), atmospheric stability (L), mean wind speed (
$\bar u\left(z \right)$ ) at height (z), and standard deviation values (σu, σv, σw) for velocities in three directions. According to Wang et al. (2008) and Wang and Yang (2010b), the mean wind speed and three standard deviations can be calculated using a similarity theory from the inputs u*, L, and height z (Stull, 2012). Following Wang et al. (2008), we use the calculated standard deviations as the default. The proposed non-Gaussian model has more inputs, including the target skewness, SI,j(z), and kurtosis, KI,j(z) for the j-direction at height z. -
In the experiment, we design three wind field simulations: (1) section 3.3.1 simulates the velocity distribution at different heights under different atmospheric conditions to assess the correctness and stability of the proposed non-Gaussian LS model; (2) section 3.3.2 provides a 1D homogeneous stationary field for wind trajectory simulation, aiming to investigate how the skewness and kurtosis in simulated wind velocities affect its displacement (i.e., the final dispersion distance) distribution; and (3) section 3.3.3 applies the non-Gaussian LS model to simulate particle dispersion in a 3D inhomogeneous, non-stationary wind field, comparing the differences in particle concentration with that in the Gaussian model.
-
The well-mixed condition criterion requires an LS model to generate a correct steady distribution of wind velocity in the position-velocity phase space (Thomson, 1987; Thomson and Wilson, 2012). To test the well-mixed condition, we verify if the Lagrangian velocity statistics of fluid particle trajectories simulated by a model are equal to the Eulerian statistics. Namely, we investigate how the computed velocity PDFs are in agreement with the measured values.
Specifically, we simulate 448 measured periods of wind velocities at eight different heights in 30 min, and then calculate some statistics of the simulated velocities, including distribution characteristics (mean, variance, skewness, kurtosis) in three directions and friction velocity (u*). Note that the settling speed, vs, is set at zero because no particle is applied in the wind dispersion.
The accuracy of each statistic, Y, as compared with the measured one, X, is assessed by using the linear regression analysis, Y=kX (Wang and Yang, 2010b). Additionally, the coefficient of determination (R2) of the regressed linear function is also used to show the proportion of the measured data that could be explained by the simulation. If both slope k and coefficient R2 are close to 1, an LS model achieves better simulation accuracy. In this study, we compare the performance between Gaussian and non-Gaussian LS models in terms of the slopes and coefficients of all statistics. To further analyze the stability of the non-Gaussian LS model, we repeat the wind velocity simulation 50 times and list the mean and standard deviation of its performance in all linear regression analysis results.
-
To investigate the difference in the trajectory affected by skewness and kurtosis in the simulated velocities, we conduct a wind dispersion simulation in a 1D homogeneous stationary wind field. Under this setting, we simulate 30 000 trajectories for three types (V1, V2, V3) of velocity distributions with the same mean (0) and variance (1) but with different combinations of skewness (V1 = 0, V2 = 0, V3 = 0.5) and kurtosis (V1 = 3, V2 = 6, V3 = 6). For each trajectory, we simulate the total simulation time T to be 30 min, and we set the short time dt for each step to equal 0.006 s (minimum of calculated①
dt for all measured atmospheric conditions) to control its influence on wind movements. We use the minimum dt because a longer dt will miss the turbulence at the shorter dt. After the total simulation time runs out, we record wind displacements for all trajectories and compute the distribution characteristics (mean, variance, skewness, and kurtosis) of the wind displacement (summation of all flight segment distances during T) for each type of wind dispersion. Finally, the displacement distributions of three types of wind dispersion are compared to analyze the influence of skewness and kurtosis on wind velocities. -
To further analyze the differences in trajectories generated by the Gaussian versus the non-Gaussian LS models in a more complicated environment, we apply two models to particle dispersion simulation in a 3D inhomogeneous non-stationary wind field, as in Wang and Yang (2010b). Details are as follows:
Particle dispersion: In the simulation, a source area (a circular area with radius = 3 m) is divided radially (n = 60) and angularly (m = 72) into sectors of area dAnm. For each sector, Np = 30 particles are released sequentially and independently at a height of 1.5 m with a source strength of Q0 = 10 grains m−2 s−1. During a short time step, dt, the 3D instantaneous velocities (u, v, and w) are generated by a Gaussian or non-Gaussian LS model. Also, the settling speed vs of this particle is set to be 0.0165 m s−1. To simulate an inhomogeneous wind field, we divide the entire wind field into eight homogeneous layers, based on the middle lines of eight heights (3.25, 7.5, 15, 25, 35, 45, 52.5 m), where measured wind data at a certain height represent the atmospheric condition within that layer. In total, we have wind data for 448 sets at eight heights. Note that we use the measured mean and standard deviation in three directions as model inputs instead of the calculated mean and deviation, as referred to in section 3.3.2, to avoid a biased conclusion drawn from calculation errors for these inputs. Moreover, as the original coordinate system (X, Y, Z) of measured wind data is rotated into the mean wind direction with an angle θ (Fig. 1a), we convert the position of simulated particles to the original coordinate system by X=xcosθ−ysinθ, Y=xsinθ+ycosθ, and Z=z.
Particle deposition: Particle dispersion stops when the study time ends (30 minutes), the particle is deposited on the ground, or it flies out of the simulation space (X, Y, or Z are larger than 100 m). Following Wang et al. (2008), the particle will reach the ground during the time step dt if the height z of a particle at the beginning of a time step is within the range of 0 < z < (−w+vs)dt. The chance to be deposited (PG) equals 2vs/(vs−w) if w≤−vs or PG=1 if |w|<vs. To determine whether the particle will deposit on the ground, a uniform random number (Rn) that ranges from 0 to 1 is used. Specifically, the particle touches the ground and stops dispersing if Rn is less than the deposition chance PG; otherwise, the particle is reflected at a new height (z) and |zt-1-2vsdt| keeps on moving, where zt-1 is the previous position of this particle at time t − 1.
Particle concentration: To record the particle concentration
$c\left({x,y,z,\Delta t} \right)$ at a certain point (x,y,z) during time period Δt, a detection cube is defined with the side length sl=0.09 m centered on the point with volume Δt=sl3. We set detectors at every integer coordinate in the simulation space, excluding the source area, at six different heights (1, 2, 4, 8, 16, 32 m). Each time a particle from sector nm spends time (Δt) within a detector at position (x,y,z), a weighted residence time accumulator Tj(x,y,z) is incremented by δtdAnm. After all particles from all source sectors have flown, the mean concentration${\rm{c}}\left({x,y,z,\Delta t} \right)$ during the simulation time period Δt is calculated by${Q_0}{T_j}\left({x,y,z} \right)/\Delta V{N_p}$ .
3.1. Experiment datasets
3.2. Model inputs
3.3. Wind field simulation
3.3.1. Wind velocity simulation
3.3.2. Wind trajectory simulation
3.3.3. Particle concentration simulation
-
The well-mixed condition criterion requires an LS model to stably generate the correct wind distribution. To meet this requirement, we verify the proposed model using a wind turbulence simulation, as mentioned in section 3.3.1. We analyze the accuracy, stability, and adaptability of the proposed model as follows:
Accuracy of velocity skewness and kurtosis: Figure 2 illustrates the linear regression analysis for four distribution characteristics (mean E, variance V, skewness S, and kurtosis K) of wind velocities simulated by Gaussian (g) and non-Gaussian (ng) models in three directions (u, v, w) at eight different heights. We observed that the Gaussian and non-Gaussian models perform similarly in simulating the mean and variance of wind velocities, as the theory proved in section 2.2. However, the non-Gaussian model substantially outperforms the Gaussian model in skewness (k∈[0.95, 1.03], R2∈[0.91, 0.97] and kurtosis (k∈[0.94, 1.05], R2∈[0.89, 0.94]). These results indicate that, compared with the Gaussian model, the proposed model can largely improve the accuracy of skewness and kurtosis in simulated velocities while maintaining the precision in mean and variance. Also, the non-Gaussian model can generate wind velocities with better distribution accuracy.
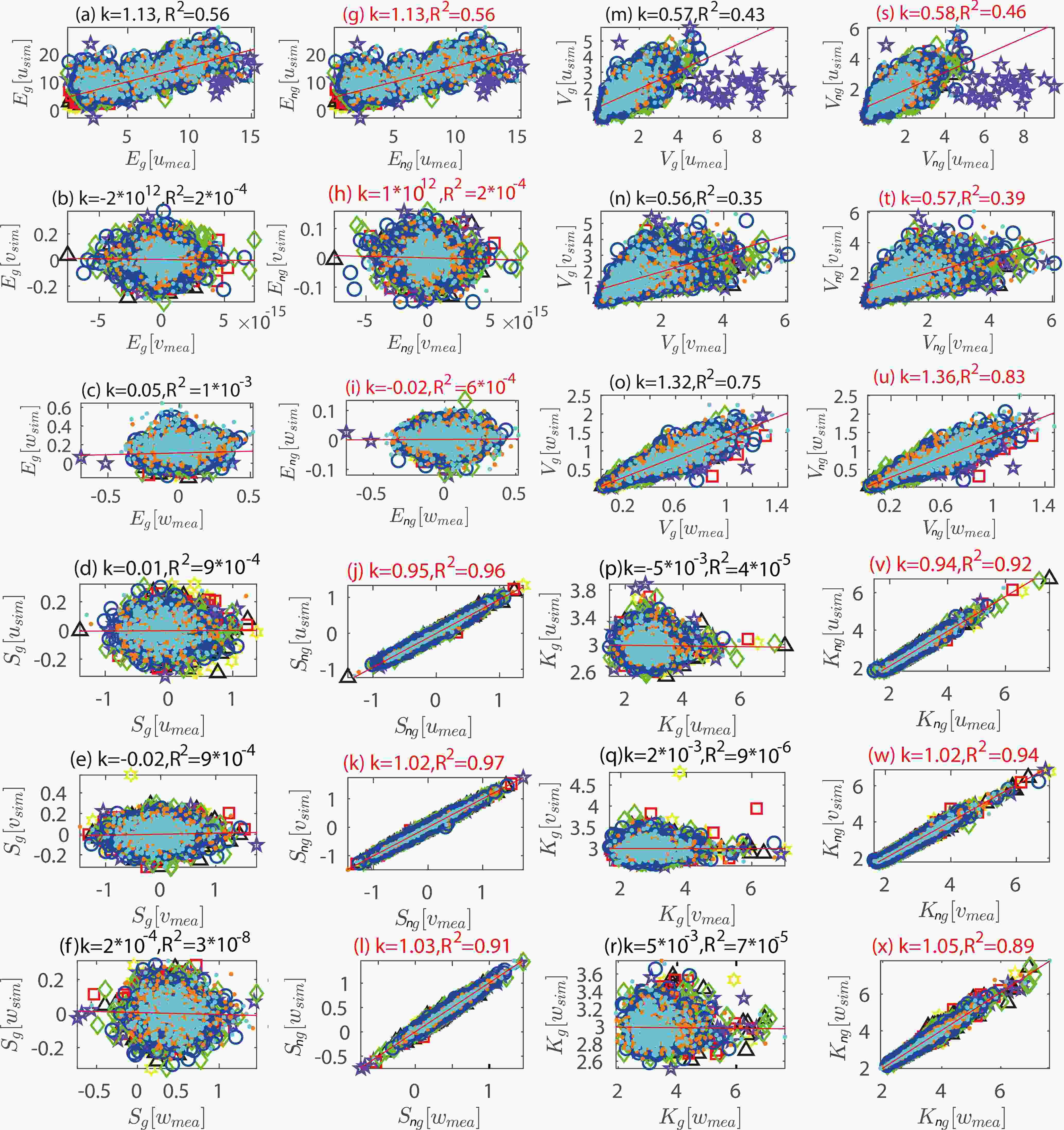
Figure 2. Regression analysis on the mean (E), variance (V), skewness (S), kurtosis (K) of the simulated velocities by the Gaussian (g) and non-Gaussian (ng) models in three wind directions (u, v, w) at eight heights (z), where the simulated (sim) statistics are compared with the measured (mea) ones. Units of velocity: m s−1. This figure shares the same legend as Fig. 3.
Moreover, to compare the time history wind velocities between field measurements and simulations, we first calculated the Welch’s power spectral density estimate for all pairs of measured wind velocities and simulated ones by a model (Gaussian and non-Gaussian), then tested the statistical difference between 10752 pairs (448 30-min periods × 8 heights × 3 wind directions) of spectral density distributions by using the Wilcoxon signed-rank test (Wilcoxon, 1945) at a 5% significance level. Also, we used the Cliff’s delta (δ, a non-parametric effect size measure) to quantify the amount of difference between two models (Cliff, 2014). As shown in Table 3, δ ranges from −1 to 1, and its value range is divided into four effectiveness level, where a higher level indicates that two models have a greater concentration difference.
Level Cliff’s delta (|δ|) Effectiveness level 1 0.000 ≤ |δ| < 0.147 Negligible 2 0.147 ≤ |δ| < 0.330 Small 3 0.330 ≤ |δ| < 0.474 Medium 4 0.474 ≤ |δ| < 1.000 Large Table 3. Cliff’s delta and the effectiveness level.
Table 4 shows that for the Gaussian model, 10 536 of its generated spectral density distributions have no significant difference (i.e., p-values ≥ 0.05) with those of measured ones, where only 4925 of them show large effect size. In contrast, with the non-Gaussian model, all spectral density distributions between simulation and measurements have no difference in statistical significance, while nearly all of them show large effect size. These results imply that the time history velocities simulated by the non-Gaussian model have strong correlation with the measured ones.
Model Statistical difference (p < 0.05) No statistical difference (p ≥ 0.05) Negligible effect size Small effect size Negligible effect size Large effect size Gaussian 216 1418 1932 2261 4925 Non-Gaussian 0 0 0 23 10 728 Table 4. Statistical comparisons of spectral density functions between measured wind velocities and simulated velocities by a Gaussian or non-Gaussian model.
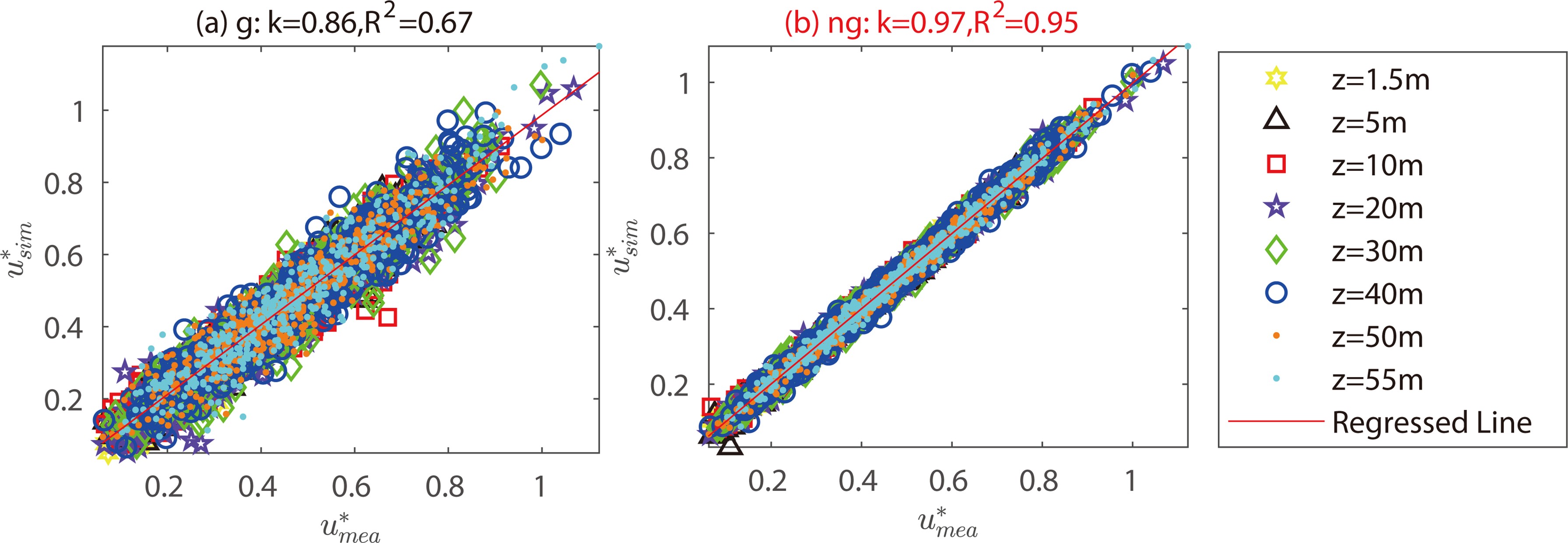
Accuracy of friction velocity: Figure 3 shows the linear regression analysis for friction velocity (u*) simulated by two LS models. The results indicate that the non-Gaussian model achieves greater accuracy in simulating friction velocities (k = 0.97, R2 = 0.95) than the Gaussian model (k = 0.86, R2 = 0.67), apparently because of the improvements in skewness and kurtosis. The friction velocity represents the coupling between wind velocities, u, v, and w, reflecting the true dispersion behaviors of wind turbulence. These results also suggest that the non-Gaussian model can better simulate wind turbulence behaviors at different heights.
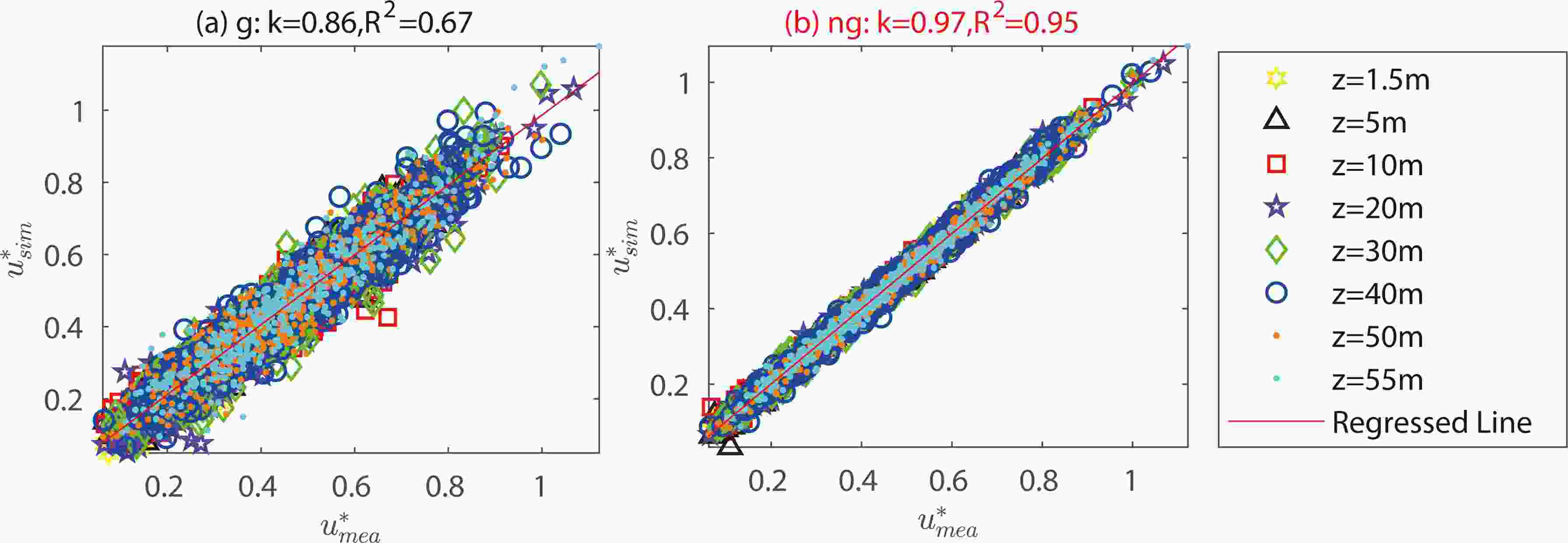
Figure 3. Regression analysis on the friction velocity (u*) of the simulated velocities by the Gaussian (g) and non-Gaussian (ng) models at eight heights (z), where the simulated (sim) statistics are compared with the measured (mea) ones. Units: m s−1.
Model stability: To investigate whether the non-Gaussian model can stably generate the velocity distribution that appears above, we repeat the wind velocity simulation 50 times. Table 5 provides the mean and standard deviation of the linear regression results in slope (k) and coefficient of determination (R2). In the table, the results are presented by k (R2). S1 is the original result of Fig. 2, and S4 is the result of 50 repetitions. Notably, S4 has mean values that are close to the results of S1 with a small standard deviation, indicating that the non-Gaussian model can provide stable wind turbulence simulation. The accuracy and stability of the non-Gaussian LS model implies that the proposed model better simulates wind trajectories in the field, based on the well-mixed condition criterion.
Setting Mean Variance u v w u v w S1 1.13 (0.56) 1e12 (2e-4) −2e-2 (6e-4) 0.58 (0.46) 0.57 (0.39) 1.36 (0.83) S2 1.13 (0.56) −2e12(5e-4) 2e-2 (5e-4) 0.57 (0.46) 0.57 (0.39) 1.36 (0.83) S3 1.13 (0.56) 6e11 (1e-3) 4e-3 (1e-3) 0.58 (0.46) 0.57 (0.39) 1.37 (0.84) Mean of S4 1.13 (0.56) −3e9 (4e-4) 4e-4 (3e-4) 0.57 (0.46) 0.57 (0.39) 1.36 (0.83) Std of S4 7e-4 (5e-4) 2e12 (5e-4) 2e-2 (4e-4) 2e-3 (2e-3) 2e-3 (2e-3) 4e-3 (2e-3) u* Skewness Kurtosis u v w u v w 0.97 (0.95) 0.95 (0.96) 1.02 (0.97) 1.03 (0.91) 0.94 (0.92) 1.02 (0.94) 1.05 (0.89) 0.42 (0.58) 1.01 (0.97) 1.02 (0.97) 1.03 (0.91) 1.01 (0.92) 1.04 (0.93) 1.05 (0.89) 0.86 (0.97) 1.01 (0.98) 1.02 (0.97) 1.01 (0.93) 1.01 (0.94) 1.04 (0.93) 1.00 (0.89) 0.97 (0.95) 0.95 (0.96) 1.02 (0.97) 1.03 (0.91) 0.95 (0.92) 1.03 (0.93) 1.04 (0.88) 4e-3 (2e-3) 3e-3 (1e-3) 4e-3 (1e-3) 7e-3 (3e-3) 1e-2 (7e-3) 1e-2 (6e-3) 1e-2 (7e-3) Table 5. Performance comparison of non-Gaussian model with three different settings: S1, origin; S2, remove pw from u; S3, remove historical effects in three directions (e.g., qu=ru); S4, repeat the original setting 50 times. Units of velocity (u, v, w) and friction velocity (u*): m s−1.
Sensitivity analysis on the u–w coupling term: As described in section 2.3, we add the term pw in u of Eq. (9) to strengthen the u–w coupling, as with the traditional Gaussian LS model; therefore, we analyze its necessity in S2 of Table 5. Results show that removing pw and its associated coefficients (cu and cw) has a negligible effect on four distribution characteristics, but the accuracy of friction velocity largely decreases. Therefore, the pw term and its coefficients are required for the non-Gaussian model.
Sensitivity analysis on the historical effects in velocities: Eq. (9) shows that our non-Gaussian model is a combination of a non-Gaussian variable (pu, pv or pw) and a Markov term (qu, qv or qw) with historical effects on velocities. The results of S3 in Table 5 investigates the model performance without the historical effects—namely, keeping only the random term (ru, rv, or rw) in each Markov process. Results indicate that by removing the historical effects in equations, significant decreases occur in the friction velocity (slope reduces to 0.86), which implies that keeping the original Markov terms in the proposed non-Gaussian model is necessary.
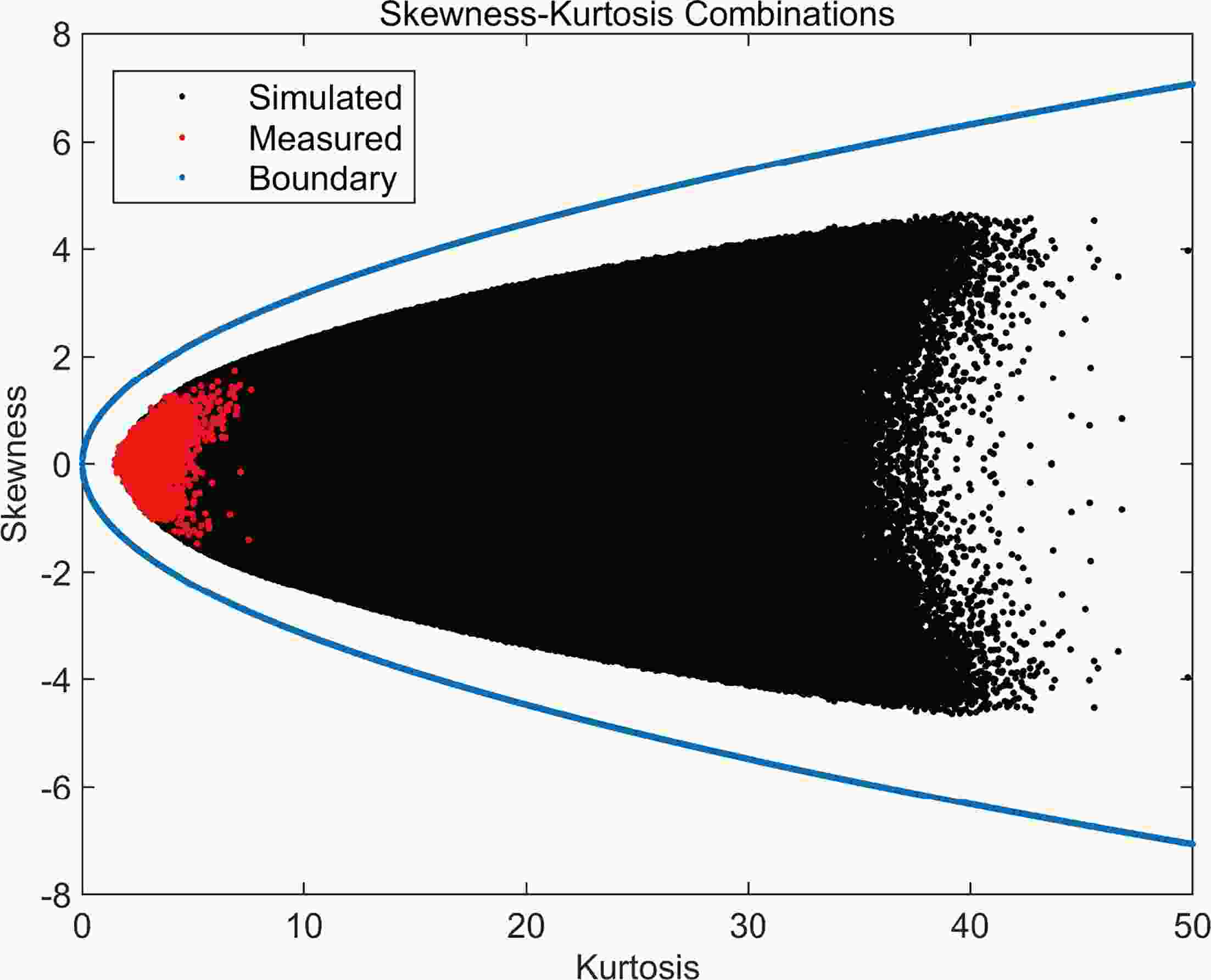
Model adaptability: Because of the non-stationarity of the LS model, the simulated wind velocity distributions in each simulation period must accommodate many different types of measured non-Gaussian distributions, in terms of a wide range of skewness–kurtosis combinations. To explore the coverage of skewness–kurtosis combinations, we generated all possible results for the non-Gaussian model implemented in Eq. (3) in section 2.3.2. We also compare these results with a limited range of the skewness–kurtosis combinations suggested by Feller (1966), who stated that the skewness (S) is determined by the kurtosis (K), where S2≤K.
Figure 4 shows that the skewness–kurtosis combinations produced by the non-Gaussian model (the black points) can cover most of the measured combinations (the red spots) with a negligible deviation and largely approach the theoretical boundary (the blue dots) referred to by Feller (1966). The boundary gap results from the limited scope of the parameters in the setting, such that the combination coefficient was constrained from 0.1 to 0.9, as referred to in section 2.3.2. In brief, the non-Gaussian model adapts to various non-Gaussian wind fields with a wide range of skewness–kurtosis combinations.
-
Section 4.1 implies that improved skewness and kurtosis in the simulated velocities from the non-Gaussian model can produce a better trajectory simulation. To investigate how these third- and fourth-order wind velocities affect its trajectory in the field, we conduct a 1D homogeneous wind field simulation as the setting, as in section 3.3.2.
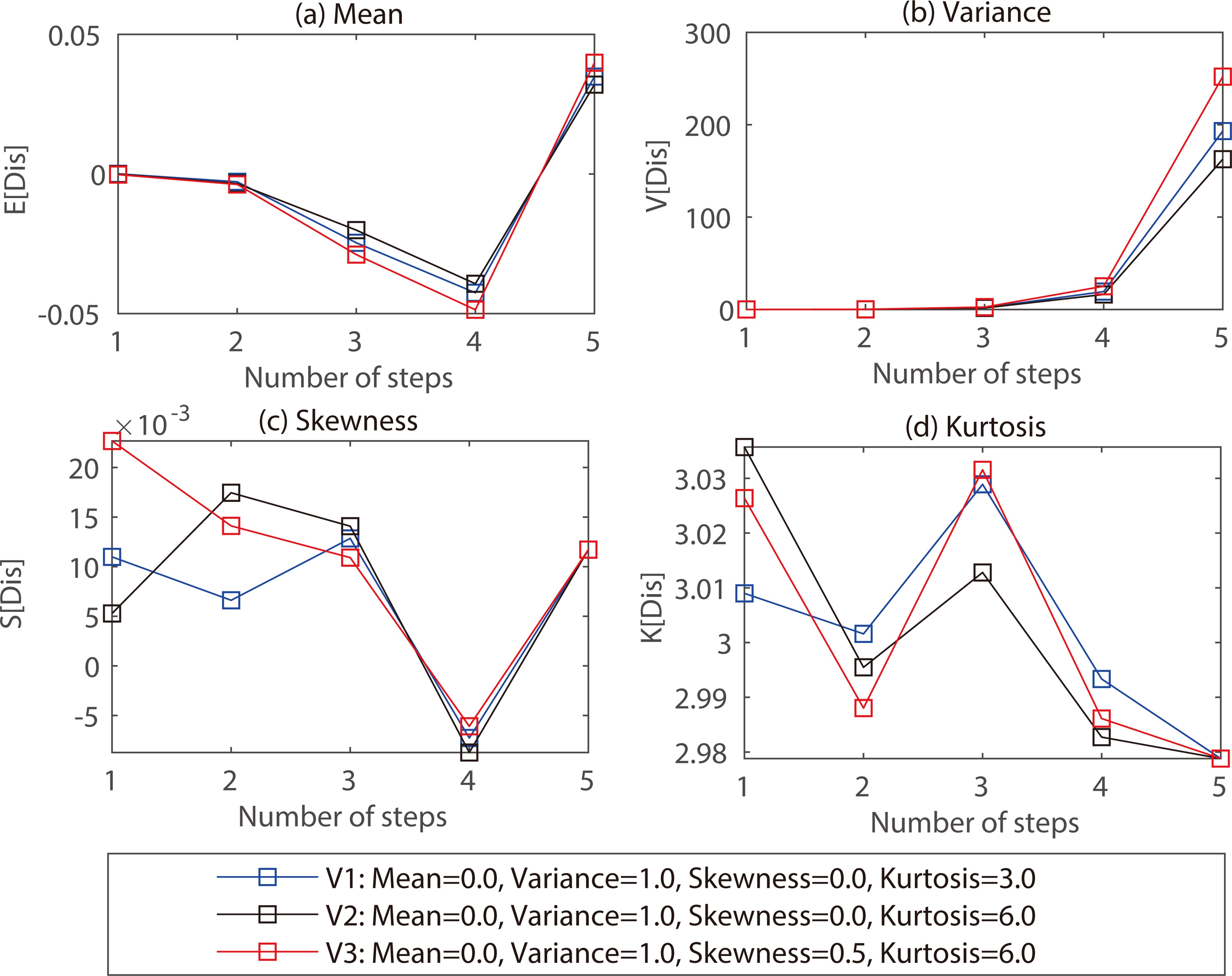
Figure 5 illustrates four distribution characteristics (mean, variance, skewness, kurtosis) of wind displacements with three types of wind velocity distributions (V1, V2, and V3), where the simulated velocities of V1 follow the standard Gaussian distribution (skewness = 0, kurtosis = 3); V2 generates a velocity distribution with a higher kurtosis (6); and V3 adds skewness (0.5) to the V2.
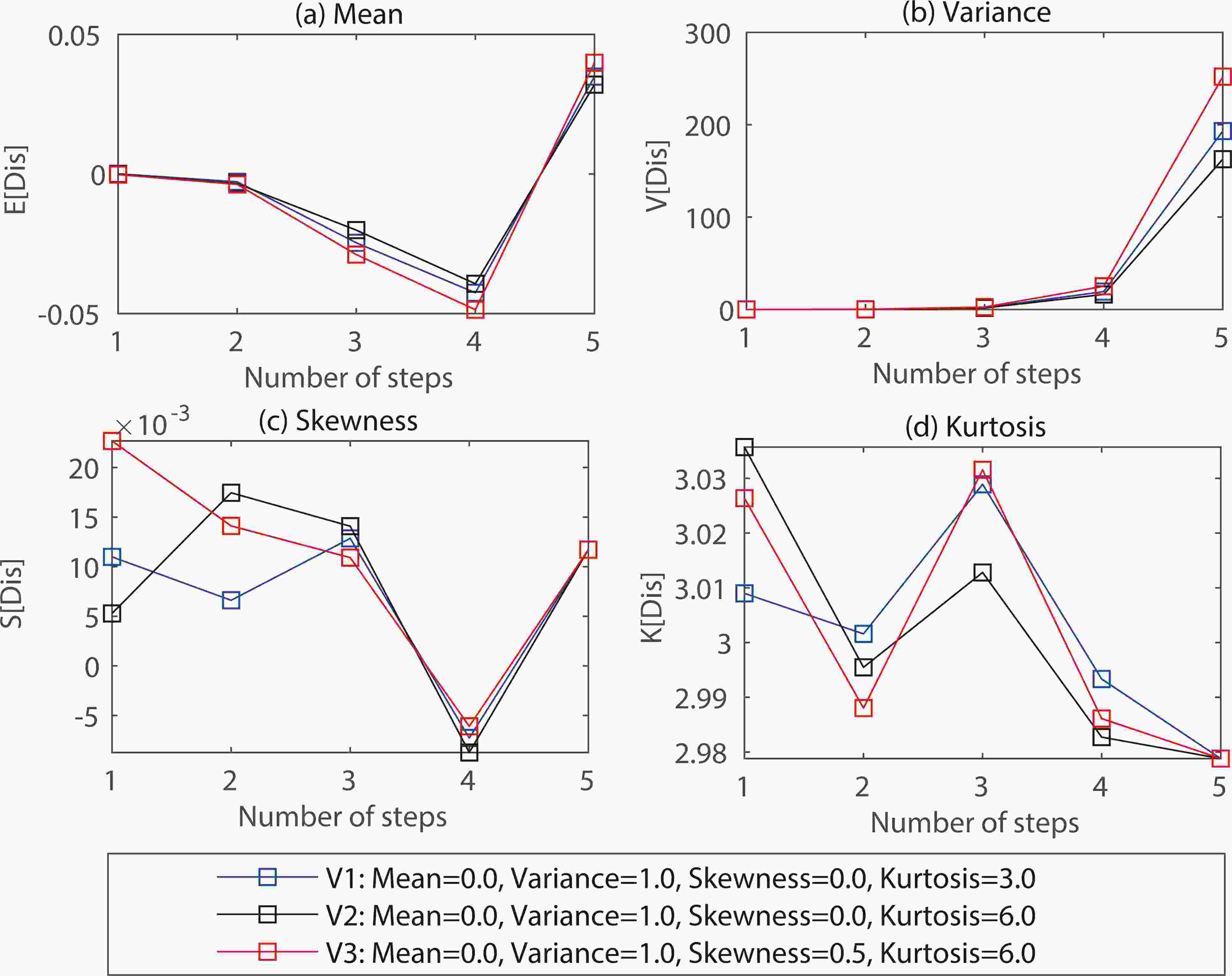
Figure 5. Four statistical characteristics of wind displacement (Dis) distribution, including mean (M), variance (V), skewness (S), and kurtosis (K), with different number of total steps, driven by three types of velocity distributions (V1, V2, V3) in terms of the same mean/variance (E/V) and different skewness/kurtosis (S/K). Statistical differences between two displacement distributions are estimated by the two-sample Kolmogorov–Smirnov test at a 5% significance level, and any two displacement distributions with the same total steps are significantly different (p-value < 0.001). Units for the mean and variance of the displacement are m and m2, respectively, while the skewness and kurtosis of the displacement are dimensionless.
Figures 5c and d show that as the number of steps increases, the skewness and kurtosis of the three displacement distributions converge to 0 and 3, respectively. These results indicate that in the long run, the simulated displacement is Gaussian, even if the wind velocity is non-Gaussian.
Additionally, Fig. 5a shows the mean of three displacement distributions. Note that their mean values are slightly biased from zero. However, in theory, their mean should equal zero for a wind velocity with a mean of zero. This condition may result from the PRNGs used in the LS model, which cannot strictly output a sequence of random numbers with a mean of zero. Certainly, the mean velocity is usually not zero, where the measured mean ranges from 0.13 to 15.23 (Table 2). Hence, this little bias in mean displacement is acceptable for practical simulation.
Figure 5b shows that the variance of simulated displacement gradually increases as the total number of steps rises. We can observe that the V2 with a higher kurtosis has a lower variance than the V1, which suggests that a higher velocity kurtosis leads to a lower displacement variance. This implication is because a higher kurtosis means the simulated velocities are more likely to be close to zero. Moreover, incorporating skewness in the V3 causes a higher displacement variance. We also note that when the skewness is large, such as 0.5 in this example, the increased displacement variance of the skewed velocity strongly counteracts the decreased displacement variance by the higher velocity kurtosis. Thus, skewness is more influential than kurtosis on variances of the displacement distribution.
Figure 5 also estimates the statistical difference between displacement distributions with different total steps by using a two-sample Kolmogorov–Smirnov test (Massey, 1951) at a 5% significance level. Results show that all pairs of distribution comparisons are significantly different (p-value < 0.001), implying that the improved skewness and kurtosis in velocities lead to a substantially different displacement distribution. This difference suggests the necessity and utility of developing a non-Gaussian model to perform wind field simulations.
-
Section 4.2 indicates that the improved skewness and kurtosis in the simulated velocity mainly affect its displacement variance in a simplified and ideal wind field. An investigation of how the skewness and kurtosis affect particle concentration simulations in a more complicated environment is worth pursuing. Hence, we conduct 448 dispersion simulations in a 3D inhomogeneous wind field with different weather conditions, as noted in section 3.3.3.
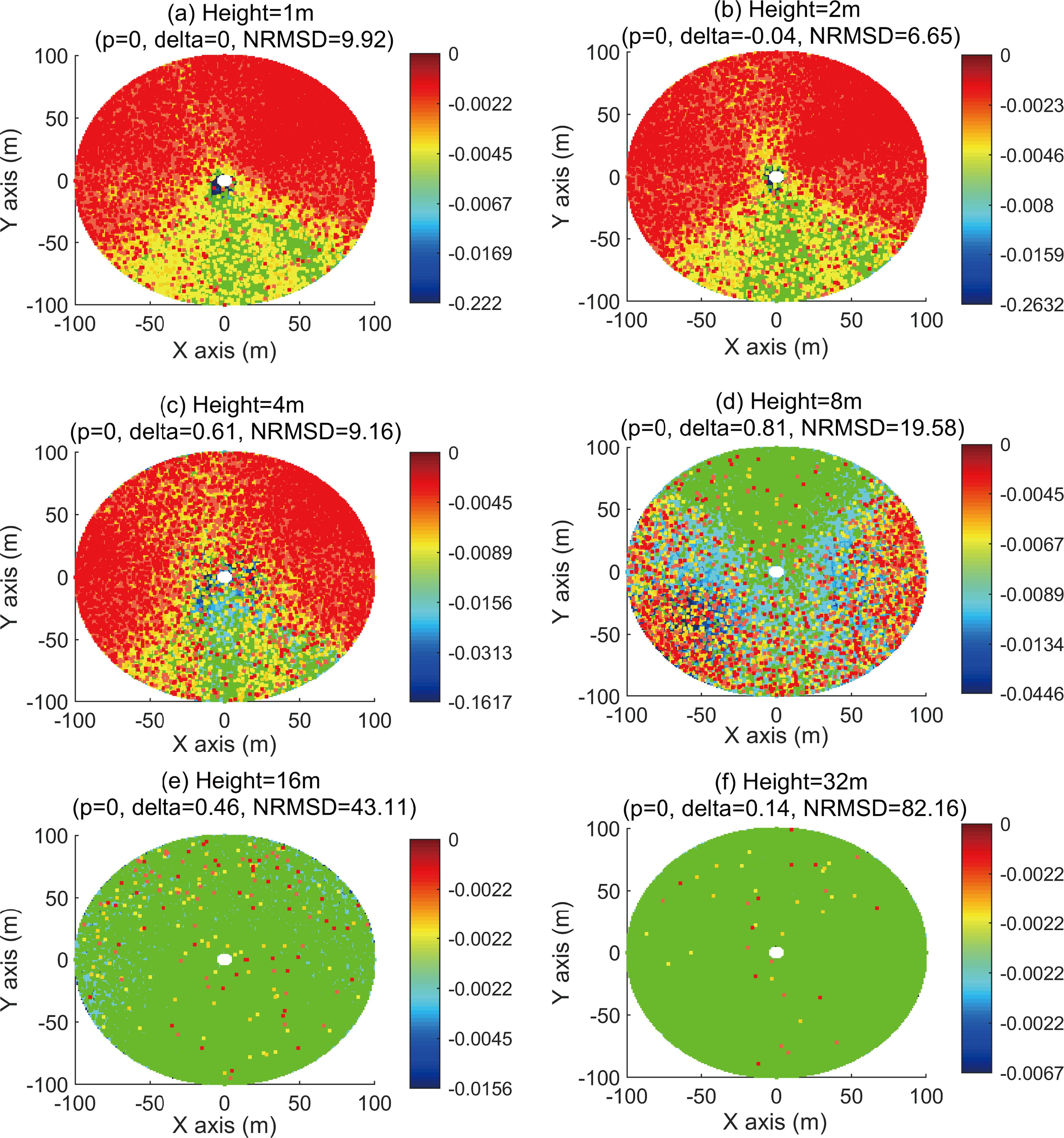
For the dispersion simulations, we compare the concentration values generated by the two models at six different heights (1, 2, 4, 8, 16, and 32 m), where the difference is calculated as a non-Gaussian model-simulated concentration minus that of the Gaussian model, and then normalizing the results by the Gaussian model. Figure 6 illustrates the average of 448 concentration percentage values at each position. Results show that the average concentration percentage values between the two models are largely different in most areas because of the difference in the skewness and kurtosis of simulated particle velocities.
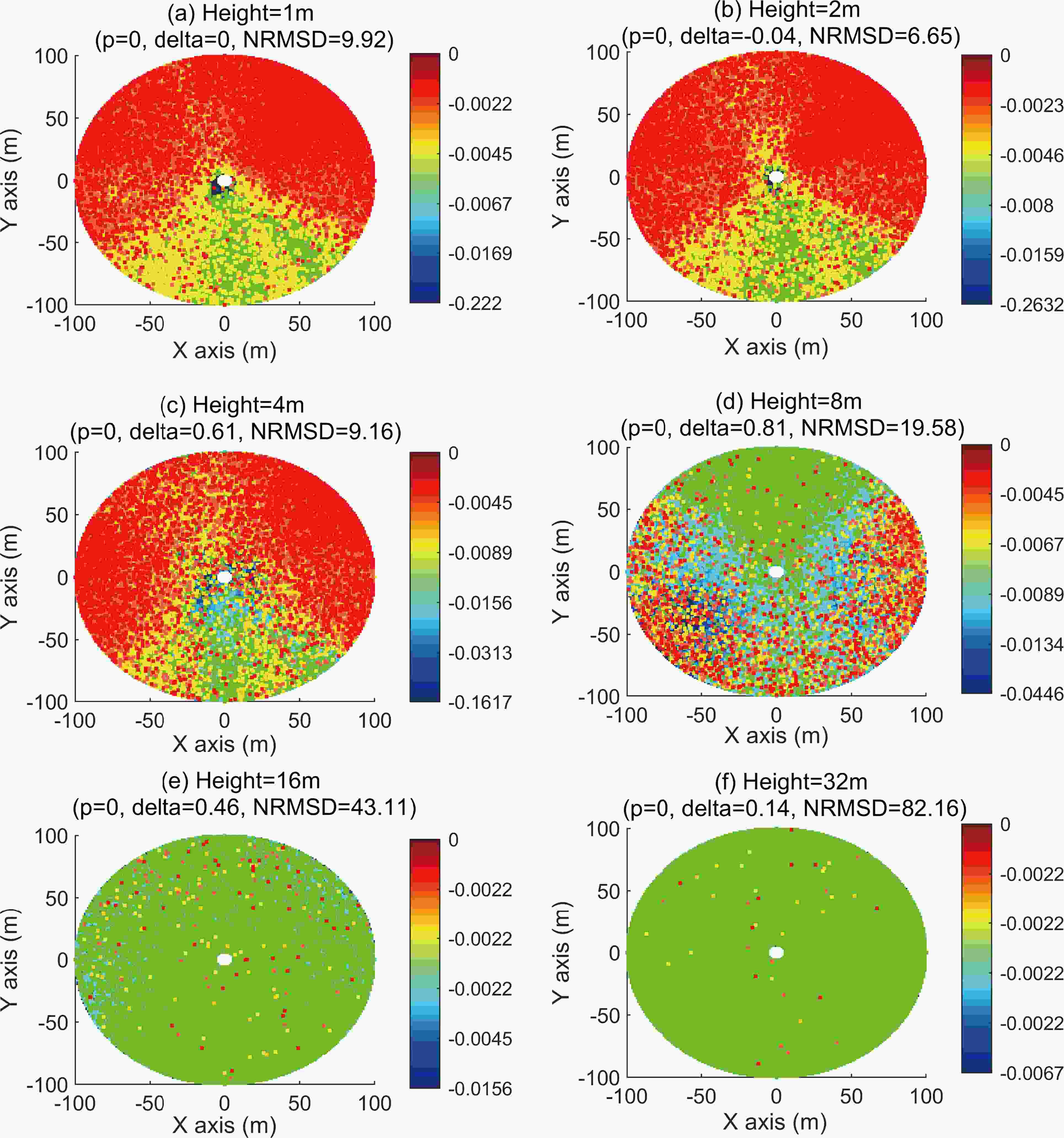
Figure 6. The average concentration percentage differences between Gaussian and non-Gaussian models with 448 different 30-min weather conditions at six different heights, where each dot in a figure represents the percentage of the concentration difference (non-Gaussian model simulated concentration minus the Gaussian’s, then normalized by the Gaussian’s); the p-value denotes the statistical difference between concentrations generated by two models by the Wilcoxon signed rank test at a 5% significance level; the delta value indicates the size effect of statistical difference.
To compare the overall concentration difference between two models, we estimated their statistical difference by performing the Wilcoxon signed-rank test (Wilcoxon, 1945) at a 5% significance level (i.e., p < 0.05 indicates a significant difference) on the paired concentration values at six heights. This test does not assume that the paired data follow a Gaussian distribution necessarily. Figures 6a–f show that all p-values are less than 0.05, indicating that concentrations produced by two models are substantially different. Moreover, we used Cliff’s delta (δ, a non-parametric effect size measure) to quantify the amount of difference between the two models (Cliff, 2014). As shown in Table 3, δ ranges from −1 to 1, and its value range is divided into four effectiveness levels, where a higher level indicates that two models have a greater concentration difference. Results in Fig. 6 show the concentration difference is large (|δ|≥0.474) at a height of 4 m (δ = 0.61) and 8 m (δ = 0.81), medium (0.33 ≤|δ|< 0.474) at a height of 16 m (δ = 0.46), and negligible (|δ| < 0.147) at other heights (1 m, 2 m, and 32 m). These results imply an overall concentration difference between Gaussian and non-Gaussian models in statistical significance.
Furthermore, Table 6 compares the characteristics and the statistical differences for 448 pairs of displacement distributions in three coordinate directions. The table indicates that the statistical estimation of the mean, variance, skewness, and kurtosis of displacement between the two models is significantly different; i.e., all pairs of 30-min particle displacement simulated by the two models differ substantially in statistical significance.
Measure Gaussian Non-Gaussian X Y Z X Y Z Avg[Mean] 317.96 3169.62 1175.75 64.08 2590.55 130.01 Avg[Variance] 1.73e7 7.01e6 9.13e5 1.00e7 2.63e6 3.94e4 Avg[Skewness] −0.12 −0.38 0.76 0.05 −0.36 2.40 Avg[Skewness] 3.40 3.66 3.72 2.56 3.48 10.90 Max[p-value] *** *** *** − − − Table 6. Statistical characteristics comparison of 448 pairs of displacement distributions in three coordinate directions (X, Y, Z) generated by Gaussian and non-Gaussian models. The statistical difference between each pair of displacement distributions are estimated by the two-sample Kolmogorov–Smirnov test at a 5% significance level, where *** indicates that the p-value is lower than 0.001. This table provides the average value (Avg) for distribution characteristics and the maximum value (Max) for the p-value. Units for the mean and variance of the displacement are m and m2, respectively, while the skewness and kurtosis of the displacement are dimensionless.
In summary, for a 3D inhomogeneous, non-stationary wind field, the non-Gaussian model with the correct skewness and kurtosis of particle velocities will generate significantly different particle displacement distributions than the Gaussian model, leading to a substantial difference in simulated particle concentrations. This sensitivity to the improved skewness and kurtosis of simulated particle velocities confirms the utility and necessity of the proposed non-Gaussian model.
4.1. Accuracy, stability, and adaptability of the non-Gaussian model
4.2. Impacts on wind trajectory simulation in a 1D homogeneous stationary wind field
4.3. Impacts on particle concentration simulation in a 3D inhomogeneous non-stationary wind field
-
In the surface layer, developing an LS model for a non-Gaussian wind field has long been a challenging problem because the current LS models cannot simulate wind velocities with distributions that are consistent with the measured distributions. In this article, we propose a non-Gaussian LS model built on a 3D inhomogeneous, non-stationary Gaussian model and incorporate high-order moments (i.e., skewness and kurtosis) into the simulated velocities. The proposed model is verified by 3584 sets of atmospheric conditions measured at eight heights by the CASES-99 project. Experimental results indicate that:
● The proposed model can incorporate precise skewness and kurtosis into simulated velocities while maintaining their accuracy in mean and variance, which further leads to an improved friction velocity (a coupling of 3D velocities). Thus, our model can better simulate a measured wind velocity distribution than the traditional Gaussian model.
● The proposed model can stably keep the distribution accuracy in simulated velocities for its small standard deviation for 50 simulations. Therefore, the proposed model can produce more accurate trajectories than the Gaussian model, as required by the well-mixed condition criterion.
● The non-Gaussian model can improve the velocity simulation without sacrificing other features of the traditional Gaussian model, including coupling between u–w velocities, historical effects in Markov processes, and inhomogeneity in vertical velocities.
● The non-Gaussian model can adapt to various non-Gaussian wind fields for a non-stationary environment because its simulated velocity distribution can cover a wide range of skewness–kurtosis combinations, including the measured ones.
● The improved skewness and kurtosis in simulated velocities will lead to a significantly different trajectory and concentration. Thus, it is worth applying the non-Gaussian LS model to wind field simulations. Specifically, velocity skewness and kurtosis have positive and negative effects, respectively, on the variance of the wind displacement distribution in a 1D homogeneous stationary wind field, where skewness is more influential than kurtosis. Also, skewness and kurtosis substantially affect the local arrangements for particle displacement and concentration in a 3D inhomogeneous non-stationary wind field.
Acknowledgements. The authors gratefully acknowledge the financial support for this research from a USDA-AFRI Foundational Grant (Grant No. 2012-67013-19687) and from the Illinois State Water Survey at the University of Illinois at Urbana—Champaign. The opinions expressed are those of the author and not necessarily those of the Illinois State Water Survey, the Prairie Research Institute, or the University of Illinois at Urbana—Champaign.
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.




 DownLoad:
DownLoad:






































 AAS Website
AAS Website 
 AAS WeChat
AAS WeChat